2.1 Introduction

The most significant characteristic of General Game Playing is that players do not know the rules of games before those games begin. Game rules are communicated at runtime, and the players must be able to read and understand the descriptions they are given in order to play legally and effectively.

In general game playing, information about games is typically communicated to players in a formal language called Game Description Language, or GDL. This chapter is an introduction to GDL and the issues that arise in using it to describe games.

We start the chapter with a discussion of games as discrete systems. We then introduce GDL and describe in general terms how it can be used to describe discrete systems. After that, we look at a sample game description, and we show how to simulate instances of the game using our game description. We talk about additional features of games that ensure that they are interesting. Finally, we summarize the prefix syntax for GDL used in most GGP competitions.

2.2 Discrete Systems

In General Game Playing, we concentrate on finite, synchronous games. These games take place in an environment with finitely many states, with one distinguished initial state and one or more terminal states. In addition, each game has a fixed, finite number of players; each player has finitely many possible actions in any game state, and each state has an associated goal value for each player. The dynamic model for general games is synchronous update: all players move on all steps (although some moves could be "no-ops", which do nothing), and the environment updates only in response to the moves taken by the players.

One way to conceptualize the dynamics of a game is a state graph (like the one shown below). The nodes of the graph represent states, and the arcs represent actions. For example, if the player performs action a in state s1, the world goes to state s2. Action b leads to state s3, action c leads to state s4, and action d has no effect (in other words, the world stays in the same state). In our graph, the initial state is denoted by an incoming arrow. Here s₁ is the initial state. Terminal states are denoted here by the slightly heavier circles. In this case, s₃, s₉, and s₁₁ are terminal states.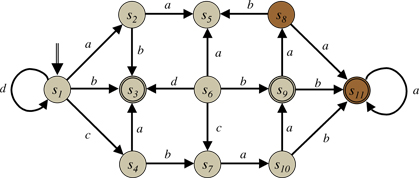

In the case of multiple players with simultaneous moves, the arcs become multi-arcs, with one multi-arc for each combination of the players' actions. Here is an example of a simultaneous move game with two players. If in state s₁ both players perform action a, we follow the arc labelled aa. If the first player does a and the second player does b, we follow the ab arc. And similarly for ba and bb.

Since all of the games that we are considering are finite, it is possible, in principle, to describe such games in the form of state graphs. Unfortunately, such explicit representations are not practical in all cases. Even though the numbers of states and actions are finite, these sets can be extremely large; and the corresponding graphs can be larger still. For example, in chess, there are thousands of possible moves and more than 10³⁰ states.

In the vast majority of games, states and actions have composite structure that allows us to define a large number of states and actions in terms of a smaller number of more fundamental entities. In Chess, for example, states are not monolithic; they can be conceptualized in terms of pieces and squares and their relationships.

The fundamental building blocks of discrete dynamic systems are entities and relations. Entities are objects presumed or hypothesized to exist in the application area of the database. Relations are properties of those objects or relationships among them. The arity of a relation is the number of objects involved in any instance of that relation.

We define a proposition to be a structure consisting of a relation with arity n together with n entities. A state corresponds to a set of propositions (those that are true in that state).

One of the benefits of formalizing games in terms of propositions is compactness. A set of n propositions corresponds to a set of 2ⁿ states (all different combinations of truth values for the n propositions). Thus, it is often possible to characterize the dynamics of games with propositions more efficiently than the corresponding state machines.

Actions are analogous to relations. An action is structure consisting of a relation with arity n together with n entities. A move is a collection of actions, one for each player in a game.

Given this propositional representation of states, we can think of the dynamics of a system in terms of how the truth values of propositions in different states change as agents perform different actions in those states. GDL is a language for expressing dynamics in this way.

2.3 Game Description Language

GDL is a logic programming language. (See Appendix 2 for details.) It is similar to other logic programming languages, such as Prolog. There are three main differences. (1) The semantics of GDL is purely declarative (there are no procedural constructs like assert, retract, and cut). (2) GDL has restrictions that assure that all questions of logical entailment are decidable. (3) There are some reserved words (described below), which tailor the language to the task of defining games.

In writing GDL descriptions, we often use object constants to represent entities. For example, in Chess, we can refer to the white king as wk, and we can refer to the the fifth file on the board as e and the third rank as 3. In some cases, we use compound terms to refer to entities. For example, we can designate the square in the fifth file and third rank as square(e,3).

In GDL, we designate propositions using object constants (for monolithic propositions) or compound terms (for propositions built up from entities and relations). For example, in Chess, we might use the object compound term on(wk,e1) to designate the proposition that the white king is on square e1.

As with propositions, we use object constants or compound terms to refer to primitive actions. For example, in Chess, we might designate the primitive action of doing nothing as noop and we might designate the action of moving a piece from square e1 to square e2 with the term move(e1,e2).

Players are the active entities in games. On each time step, each player has a set of legal actions it can perform and executes some action in this set. In GDL, we usually use object constants to refer to players, though in rare cases we use compound terms.

In GDL, the meaning of some words in the language is fixed for all games (the game-independent vocabulary) while the meanings of all other words can change from one game to another (the game-specific vocabulary).

There are 101 game-independent object constants in GDL, viz. the base ten representations of the integers from 0 to 100, inclusive, i.e. 0, 1, 2, ... , 100. These are included for use as utility values for game states, with 0 being low and 100 being high. GDL has no game-independent function constants. However, there are ten game-independent relation constants, viz. the ones shown below.

role(a) means that a is a role in the game.

base(p) means that p is a proposition in the game.

input(r,a) means that role r has action a.

init(p) means that the proposition p is true in the initial state.

true(p) means that the proposition p is true in the current state.

does(r,a) means that player r performs action a in the current state.

next(p) means that the proposition p is true in the next state.

legal(r,a) means it is legal for role r to play action a in the current state.

goal(r,n) means that player the current state has utility n for player r.

terminal means that the current state is a terminal state.

In General Game Playing, the intent is to treat a GDL description as an open logic program with the following input and output relations. (1) A GDL game description must give complete definitions for role, base, input, init. (2) It must define legal and goal and terminal in terms of an input true relation. (3) It must define next in terms of input true and does relations. Since does and true are treated as inputs, there must not be any rules with either of these relations in the head.

2.4 Game Definition Example

In our definition of Tic-Tac-Toe, states are characterized by the contents of the cells on the Tic-Tac-Toe board and control (whose turn it is to play). (It is true that control can be defined in terms of the contents of cells; but making control explicit costs little and simplifies the description.) In what follows, we use the 3-ary function constant cell together with a row m and a column n and a mark w to designate the proposition that the cell in row m and column n contains w where w is either an x or an o or a b (for blank). For example, the term cell(2,3,o) refers to the proposition asserting that there is an o in the cell in row 2 and column 3. We use the unary function constant control to map a player into the proposition that it is that player's turn to mark a cell. For example, the term control(white) refers to the proposition asserting that it is x's turn to mark a cell.

There only two types of actions a player can perform - he can mark a cell or he can do nothing (which is what a player does when it is not his turn to mark a cell). The binary function mark together with a row m and a column n designates the action of placing a mark in row m and column n. The mark placed there depends on who does the action. The object constant noop refers to the act of doing nothing.

We begin with an enumeration of roles. In this case, there are just two roles, here called x and o

    role(white)
    role(black)

We can characterize the propositions of the game as shown below.

    base(cell(M,N,x)) :- index(M) & index(N)
    base(cell(M,N,o)) :- index(M) & index(N)
    base(cell(M,N,b)) :- index(M) & index(N)

    base(control(white))
    base(control(black))

We can characterize the feasible actions for each role in similar fashio.

    input(R,mark(M,N)) :- role(R) & index(M) & index(N)
    input(R, noop) :- role(R)

    index(1)
    index(2)
    index(3)

Next, we characterize the initial state by writing all relevant propositions that are true in the initial state. In this case, all cells are blank; and the x player has control.

    init(cell(1,1,b))
    init(cell(1,2,b))
    init(cell(1,3,b))
    init(cell(2,1,b))
    init(cell(2,2,b))
    init(cell(2,3,b))
    init(cell(3,1,b))
    init(cell(3,2,b))
    init(cell(3,3,b))
    init(control(white))

Next, we define legality. A player may mark a cell if that cell is blank and it has control. Otherwise, the only legal action is noop.

    legal(W,mark(X,Y)) :-
      true(cell(X,Y,b)) &
      true(control(W))

    legal(white,noop) :-
      true(control(black))

    legal(black,noop) :-
      true(control(white))

Next, we look at the update rules for the game. A cell is marked with an x or an o if the appropriate player marks that cell. If a cell contains a mark, it retains that mark on the subsequent state. If a cell is blank and is not marked on that step, then it remains blank. Finally, control alternates on each play.

    next(cell(M,N,x)) :-
      does(white,mark(M,N)) &
      true(cell(M,N,b))

    next(cell(M,N,o)) :-
      does(black,mark(M,N)) &
      true(cell(M,N,b))

    next(cell(M,N,W)) :-
      true(cell(M,N,W)) &
      distinct(W,b)

    next(cell(M,N,b)) :-
      does(W,mark(J,K))
      true(cell(M,N,W)) &
      distinct(M,J)

    next(cell(M,N,b)) :-
      does(W,mark(J,K))
      true(cell(M,N,W)) &
      distinct(N,K)

    next(control(white)) :-
      true(control(black))

    next(control(black)) :-
      true(control(white))

Goals. The white player gets 100 points if there is a line of x marks and no line of o marks. If there are no lines of either sort, white gets 50 points. If there is a line of o marks and no line of x marks, then white gets 0 points. The rewards for black are analogous. The line relation is defined below.

    goal(white,100) :- line(x) & ~line(o)
    goal(white,50) :- ~line(x) & ~line(o)
    goal(white,0) :- ~line(x) & line(o)

    goal(black,100) :- ~line(x) & line(o)
    goal(black,50) :- ~line(x) & ~line(o)
    goal(black,0) :- line(x) & ~line(o)

Supporting concepts. A line is a row of marks of the same type or a column or a diagonal. A row of marks mean thats there three marks all with the same first coordinate. The column and diagonal relations are defined analogously.

    line(X) :- row(M,X)
    line(X) :- column(M,X)
    line(X) :- diagonal(X)

    row(M,X) :-
      true(cell(M,1,X)) &
      true(cell(M,2,X)) &
      true(cell(M,3,X))

    column(M,X) :-
      true(cell(1,N,X)) &
      true(cell(2,N,X)) &
      true(cell(3,N,X))

    diagonal(X) :-
      true(cell(1,1,X)) &
      true(cell(2,2,X)) &
      true(cell(3,3,X)) &

    diagonal(X) :-
      true(cell(1,3,X)) &
      true(cell(2,2,X)) &
      true(cell(3,1,X)) &

Termination. A game terminates whenever either player has a line of marks of the appropriate type or if the board is not open, i.e. there are no cells containing blanks.

    terminal :- line(W)
    terminal :- ~open

    open :- true(cell(M,N,b))

2.5 Game Simulation Example

As an exercise in logic programming and GDL, let's look at the outputs of the ruleset defined in the preceding section at various points during an instance of the game.

To start, we can use the ruleset to compute the roles of the game. This is simple in the case of Tic-Tac-Toe, as they are contained explicitly in the ruleset.

    role(x)
    role(o)

Similarly, we can compute the possible propositions. Remember that this gives a list of all such propositions; only a subset will be true in any particular state.

    base(cell(1,1,x))    base(cell(1,1,o))    base(cell(1,1,b))
    base(cell(1,2,x))    base(cell(1,2,o))    base(cell(1,2,b))
    base(cell(1,3,x))    base(cell(1,3,o))    base(cell(1,3,b))
    base(cell(2,1,x))    base(cell(2,1,o))    base(cell(2,1,b))
    base(cell(2,2,x))    base(cell(2,2,o))    base(cell(2,2,b))
    base(cell(2,3,x))    base(cell(2,3,o))    base(cell(2,3,b))
    base(cell(3,1,x))    base(cell(3,1,o))    base(cell(3,1,b))
    base(cell(3,2,x))    base(cell(3,2,o))    base(cell(3,2,b))
    base(cell(3,3,x))    base(cell(3,3,o))    base(cell(3,3,b))
    base(control(white))
    base(control(black))

We can also compute the relevant actions of the game. The extension of the input relation in this case consists of the twenty sentences shown below.

    input(white,mark(1,1))
    input(white,mark(1,2))
    input(white,mark(1,3))
    input(white,mark(2,1))
    input(white,mark(2,2))
    input(white,mark(2,3))
    input(white,mark(3,1))
    input(white,mark(3,2))
    input(white,mark(3,3))
    input(white,noop)

    input(black,mark(1,1))
    input(black,mark(1,2))
    input(black,mark(1,3))
    input(black,mark(2,1))
    input(black,mark(2,2))
    input(black,mark(2,3))
    input(black,mark(3,1))
    input(black,mark(3,2))
    input(black,mark(3,3))
    input(black,noop)

The first step in playing or simulating a game is to compute the initial state. We can do this by computing the init relation. As with roles, this is easy in this case, since the initial conditions are explicitly listed in the program.

    init(cell(1,1,b))
    init(cell(1,2,b))
    init(cell(1,3,b))
    init(cell(2,1,b))
    init(cell(2,2,b))
    init(cell(2,3,b))
    init(cell(3,1,b))
    init(cell(3,2,b))
    init(cell(3,3,b))
    init(control(white))

Once we have these conditions, we can turn them into a state description for the first step by asserting that each initial condition is true.

    true(cell(1,1,b))
    true(cell(1,2,b))
    true(cell(1,3,b))
    true(cell(2,1,b))
    true(cell(2,2,b))
    true(cell(2,3,b))
    true(cell(3,1,b))
    true(cell(3,2,b))
    true(cell(3,3,b))
    true(control(white))

Taking this input data and the logic program, we can check whether the state is terminal. In this case, it is not.

We can also compute the goal values of the state; but, since the state is non-terminal, there is not much point in doing that; but the description does give us the following values.

    goal(white,50)
    goal(black,50)

More interestingly, using this state description and the logic program, we can compute legal actions in this state. See below. The x player has nine possible actions (all marking actions), and the o player has just one (noop).

    legal(white,mark(1,1))
    legal(white,mark(1,2))
    legal(white,mark(1,3))
    legal(white,mark(2,1))
    legal(white,mark(2,2))
    legal(white,mark(2,3))
    legal(white,mark(3,1))
    legal(white,mark(3,2))
    legal(white,mark(3,3))
    legal(black,noop)

Let's suppose that the x player chooses the first legal action and the o player chooses its sole legal action. This gives us the following dataset for does.

    does(white,mark(1,1))
    does(black,noop)

Now, combing this dataset with the state description above and the logic program, we can compute what must be true in the next state.

    next(cell(1,1,x))
    next(cell(1,2,b))
    next(cell(1,3,b))
    next(cell(2,1,b))
    next(cell(2,2,b))
    next(cell(2,3,b))
    next(cell(3,1,b))
    next(cell(3,2,b))
    next(cell(3,3,b))
    next(control(black))

To produce a description for the resulting state, we substitute true for next in each of these sentences and repeat the process. This continues until we encounter a state that is terminal, at which point we can compute the goals of the players in a similar manner.

2.6 Game Requirements

The definitions in section 2.2 constrain GDL to game descriptions from which it is possible to compute the legal actions of all players for each state and from which it is possible to compute the next state for each state from the actions of all players. However, there are additional constraints that limit the scope of GDL to avoid problematic games.

Termination. A game description in GDL terminates if all infinite sequences of legal moves from the initial state of the game reach a terminal state after a finite number of steps.

Playability. A game description in GDL is playable if and only if every role has at least one legal move in every non-terminal state reachable from the initial state.

Winnability. A game description in GDL is strongly winnable if and only if, for some role, there is a sequence of individual individual actions of that role that leads to a terminal state of the game where that role's goal value is maximal no matter what the other players do. A game description in GDL is weakly winnable if and only if, for every role, there is a sequence of joint actions of all roles that leads to a terminal state where that role's goal value is maximal.

Well-formedness. A game description in GDL is well-formed if it terminates and is both playable and weakly winnable.

In general game playing, all well-formed single player games should be strongly winnable. Clearly, it is possible to generate game descriptions in GDL which are not well-formed. Checking game descriptions to see if they are well-formed can certainly be done in general by using brute-force methods (exploring the entire game tree); and, for some games, faster algorithms may exist. Game descriptions used in GGP competitions are always well-formed. However, in this book, we occasionally look at games that are not well-formed for reasons of simplicity or pedagogy.

2.7 Prefix GDL

The version of GDL presented here uses traditional infix syntax. However, this is not the only version of the language. There is also a version that uses prefix syntax.

Although some general game playing environments support Infix GDL, it is not universal. On the other hand, all current systems support Prefix GDL. Fortunately, there is a direct relationship between the two syntaxes, and it is easy to convert between them. There are just a few issues to worry about.

The first issue is the spelling of constants and variables. Prefix GDL is case-independent, so we cannot use capital letters to distinguish the two. Constants are spelled the same in both versions; but, in prefix GDL, we distinguish variables by beginning with the character '?'. Thus, the constant a is the same in both languages while the variable X in Infix GDL is spelled ?x or ?X in Prefix GDL.

The second issue in mapping between the formats is syntax of expressions. In Prefix GDL, all expressions are lists of components separated by spaces and enclosed in parentheses. Also, logical operators are spelled out. The following tables illustrates the mapping.

Finally, just to be clear on this, in Prefix GDL white space (spaces, tabs, carriage returns, line feeds, and so forth) can appear anywhere other than in the middle of constants, variables, and operator names. Thus, there can be multiple spaces between the components of an expression; there can be spaces after the open parenthesis of an expression and before the operator or relation constant or function constant; and there can be spaces after the last component of an expression and the closing parenthesis.

Problems

Problem 2.1: Consider the game description shown below.

Problem 2.2: More questions about the game in Problem 2.1.

Problem 2.3: For each of the following pairs of expressions, say whether the expression on the second line is a faithful translation of the expression on the first line into Prefix GDL.