1.1 Introduction

Games of strategy, such as chess, couple intellectual activity with competition. We can exercise and improve our intellectual skills by playing such games. The competition adds excitement and allows us to compare our skills to those of others.

The same motivation accounts for interest in Computer Game Playing as a testbed for Artificial Intelligence. Programs that think better should be able to win more games, and so we can use competitions as an evaluation technique for intelligent systems.

Unfortunately, building programs to play specific games has limited value in AI. (1) To begin with, specialized game players are very narrow. They can be good at one game but not another. Deep Blue may have beaten the world Chess champion, but it has no clue how to play checkers. (2) A second problem with specialized game playing systems is that they do only part of the work. Most of the interesting analysis and design is done in advance by their programmers. The systems themselves might as well be tele-operated.

All is not lost. The idea of game playing can be used to good effect to inspire and evaluate good work in Artificial Intelligence, but it requires moving more of the design work to the computer itself. This can be done by focussing attention on General Game Playing.

General game players are systems able to accept descriptions of arbitrary games at runtime and able to use such descriptions to play those games effectively without human intervention. In other words, they do not know the rules until the games start.

Unlike specialized game players, such as Deep Blue, general game players cannot rely on algorithms designed in advance for specific games. General game playing expertise must depend on intelligence on the part of the game player and not just intelligence of the programmer of the game player. In order to perform well, general game players must incorporate results from various disciplines, such as knowledge representation, reasoning, and rational decision making; and these capabilities have to work together in a synergistic fashion.

Moreover, unlike specialized game players, general game players must be able to play different kinds of games. They should be able to play simple games (like Tic Tac Toe) and complex games (like Chess), games in static or dynamic worlds, games with complete and partial information, games with varying numbers of players, with simultaneous or alternating play, with or without communication among the players, and so forth.

1.2 Games

Despite the variety of games treated in General Game Playing, all games share a common abstract structure. Each game takes place in an environment with finitely many states, with one distinguished initial state and one or more terminal states. In addition, each game has a fixed, finite number of players; each player has finitely many possible actions in any game state, and each state has an associated goal value for each player.

Given this common structure, we can think of a game as a state graph, like the one shown here. In this case, we have a game with one player, with eight states (named s₁, ... , s₈).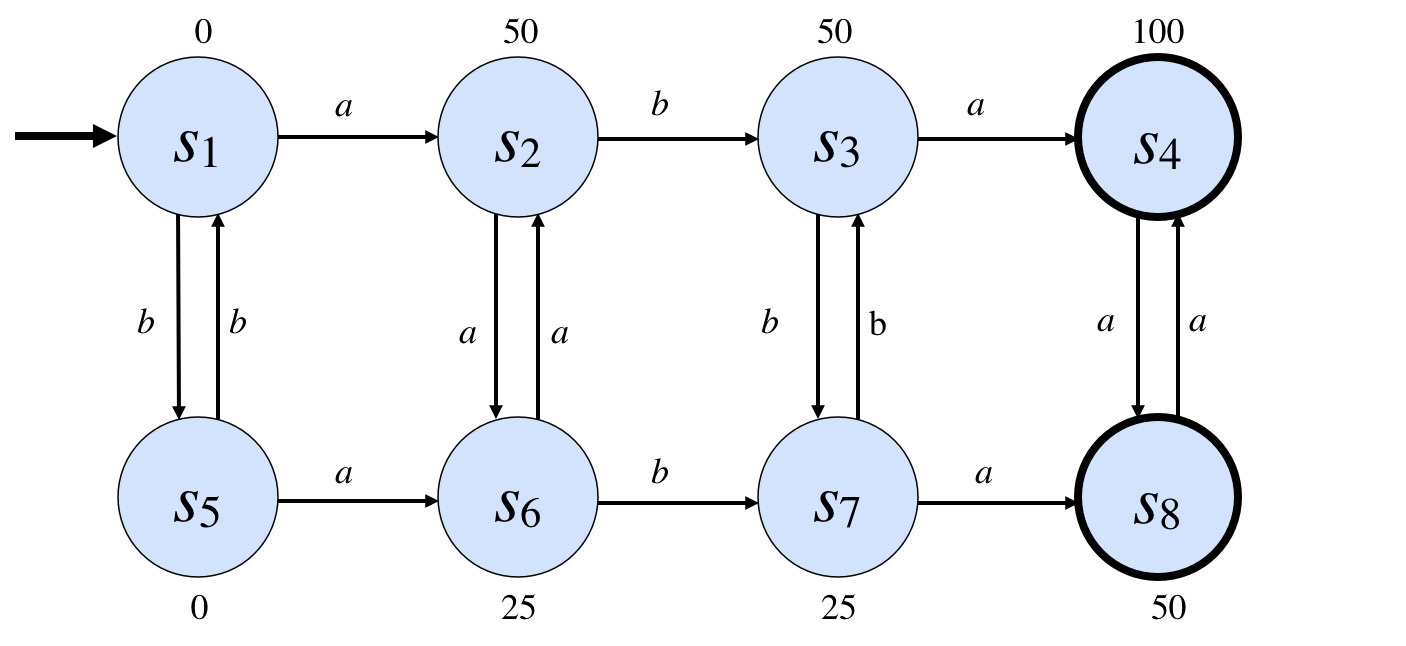

The arcs in this graph capture the transition function for the game. For example, if the game is in state s₁ and a player does action a, the game will move to state s₂. if the game is in state s₁ and a player does action b, the game will move to state s₅.

Each game has just one initial state, in this case s₁. However, there can be any number of terminal states, in this case s₄ and s₈.

The numbers associated with each state indicate the utilities of those states for the player. Players earn those scores only in terminal states. However, but they are provided for all states and in some games indicate incremental progress.

We can extend this model to accommodate games with multiple players by making two modifications. (1) We annotate each state with rewards for all players in the game. (The rewards can be the same or different for different players.) (2) For each state, we specify which player is in control, i.e. whose turn it is to play. Turns need not strictly alternate; in some cases, a single player may get several turns in a row.. (This model can be extended to games with simultaneous moves, but for the sake of simplicity, we avoid that complexity in what follows.)

This conceptualization of games is an alternative to the traditional extensive normal form definition of games as game trees. In a game tree, each node is linked to successors by arcs corresponding to the actions legal in the corresponding game state. While different nodes in game tree sometimes correspond to different states, it is possible for different nodes to correspond to the same game state. (This happens when different sequences of actions lead to the same state.)

While extensive normal form is more appropriate for certain types of analysis, the state-based representation has advantages in General Game Playing. A state-based representation makes it possible to describe games more compactly; and, since game graphs are typically much smaller than game trees, it frequently decreases the computational cost of game analysis.

1.3 Game Description

Since all of the games that we are considering are finite, it is possible, in principle, to describe such games in the form of state graphs. Unfortunately, such explicit representations are not practical in all cases. Even though the numbers of states and actions are finite, these sets can be extremely large; and the corresponding graphs can be larger still. For example, in chess, there are more than 10³⁰ possible states.

In the vast majority of games, states and actions have composite structure that allows us to define a large number of states and actions in terms of a smaller number of more fundamental entities. In Chess, for example, states are not monolithic; they can be conceptualized in terms of pieces, squares, rows and columns and diagonals, and so forth.

By exploiting this structure, it is possible to encode games in a form that is more compact than direct representation. Game Description Language (GDL) supports this by relying on a conceptualization of game states as databases and by relying on logic to define the notions of legality and so forth.

As an example of GDL, let us look at the rules for the game of Tic-Tac-Toe. Note that this example is intended as a brief glimpse at GDL, not a rigorous introduction to the language. Full details of the language are given in the next chapter.

We begin with an enumeration of roles. There are two players - x and o.

role(x)
role(o)

Next, we characterize the initial state. In this case, all cells are blank, and the x player has control..

init(cell(1,1,b))
init(cell(1,2,b))
init(cell(1,3,b))
init(cell(2,1,b))
init(cell(2,2,b))
init(cell(2,3,b))
init(cell(3,1,b))
init(cell(3,2,b))
init(cell(3,3,b))
init(control(x))

Next, we define legality. The player in control may mark a cell if that cell is blank. In GDL, symbols that begin with capital letters are variables, while symbols that begin with lower case letters are constants. The :- operator is read as "if" - the expression to its left is true if the expressions that follow it are true.

legal(mark(M,N)) :- cell(M,N,b)

Next, we look at the update rules for the game. A the player in control marks a cell, that cell contains the player's mark in the next state and the b is removed. Also, control alternates on each play. If x is in control in one state, then it is no longer in control in the next state and o is in control. If o is in control in one state, then it is no longer in control in the next state and x is in control.

mark(M,N) :: control(R)  ==> cell(M,N,R) & ~cell(M,N,b)
mark(M,N) :: control(x) ==> ~control(x) & control(o)
mark(M,N) :: control(o) ==> ~control(o) & control(x)

Goals. The x player gets a score of 100 if there is a line of x's and no line of o's. It gets 0 points if there is a line of o's and no line of x's. Otherwise, it gets 50 points. The rewards for the o player are analogous. The line relation is defined below.

goal(white,100) :- line(x) & ~line(o)
goal(white,50) :- ~line(x) & ~line(o)
goal(white,0) :- ~line(x) &  line(o)

goal(black,100) :- ~line(x) & line(o)
goal(black,50) :- ~line(x) & ~line(o)
goal(black,0) :- line(x) &  ~line(o)

Supporting concepts. A line is a row of marks of the same type or a column or a diagonal. A row of marks mean thats there three marks all with the same first coordinate. The column and diagonal relations are defined analogously.

line(Z) :- row(M,Z)
line(Z) :- column(M,Z)
line(Z) :- diagonal(Z)

row(M,X) :- cell(M,1,X) & cell(M,2,X) & cell(M,3,X)
colun(N,X) :- cell(1,N,X) & cell(2,N,X) & cell(3,N,X)
diagonal(X) :- cell(1,1,X) & cell(2,2,X) & cell(3,3,X)
diagonal(X) :- cell(1,3,X) & cell(2,2,X) & cell(3,1,X)

Termination. A game terminates whenever there is a line of marks of the same type or if the game is no longer open, i.e. there are no blank cells.

terminal :- line(x)
terminal :- line(o)
terminal :- ~open

open :- true(cell(M,N,b))

Although GDL is designed for use in defining complete information games, it can be extended to partial information games relatively easily. Unfortunately, the resulting descriptions are more verbose and more expensive to process.

1.4 Game Management

Game Management is the process of administering a game in a general game playing setting. More properly, it should be called match management, as the issue is how to manage individual matches of games, not the games themselves. However, everyone seems to use the phrase Game Management, and so we are stuck with it.

The process of running a game goes as follows. Upon receiving a request to run a match, the Game Manager's first sends a start message to each player to initiate the match. Once game play begins, it sends play messages to each player to get their plays and simulates the results. This part of the process repeats until the game is over. The Manager then sends stop messages to each player.

The start message lists the name of the match, the role the player is to assume (e.g. white or black in chess), a formal description of the associated game (in GDL), and the start clock and play clock associated with the match. The start clock determines how much time remains before play begins. The play clock determines how much time each player has to make each move once play begins.

Upon receiving a start message, each player sets up its data structures and does whatever analysis it deems desirable in the time available. It then replies to the Game Manager that it is ready for play.

Having sent the start message, the game manager waits for replies from the players. Once it has received these replies OR once the start clock is exhausted, the Game Manager commences play.

On each step, the Game Manager sends a play message to each player. The message includes information about the actions of all players on the preceding step. (On the first step, the argument is nil.)

On receiving a play message, players spend their time trying to decide their moves. The player in control must reply within the amount of time specified by the match's play clock.

The Game Manager waits for replies from the players. If the player in control does not respond before the play clock is exhausted, the Game manager selects an arbitrary legal move. In any case, once the player in control replies or the play clock is exhausted, the Game manager takes the specified move or the legal move it has determined for the player in control and determines the next game state. It then evaluates the termination condition to see if the game is over. If the game is not over, the game manager sends the move it has assumed to all players and the process repeats.

Once a game is determined to be over, the Game Manager sends a stop message to each player with information about the last move made by the player in control. The stop message allows players to clean up any data structures for the match. The information about previous plays is supplied so that players with learning components can profit from their experience.

Having stopped all players, the Game manager then computes the rewards for each player, stores this information together with the play history in its database, and ceases operation.

1.5 Game Playing

Having a formal description of a game is one thing; being able to use that description to play the game effectively is something else. In this section, we examine some of the problems of building general game players and discuss strategies for dealing with these difficulties.

Let us start with automated reasoning. Since game descriptions are written in logic, it is obviously necessary for a game player to do some degree of automated reasoning.

There are various choices here. (1) A game player can use the game description interpretively throughout a game. (2) It can map the description to a different representation and use that interpretively. (3) It can use the description to devise a specialized program to play the game. This is effectively automatic programming.

The good news is that there are powerful reasoners for Logic freely available. The bad news is that such reasoners do not, in and of themselves, solve the real problems of general game playing, which are the same whatever representation for the game rules is used, viz. dealing with indeterminacy and resource bounds.

The simplest sort of game is one in which there is just one player and the number of states and actions is not too large. For such cases, traditional AI planning techniques are ideal. Depending on the shape of the search space, the player can search either forward or backward to find a sequence of actions / plays that convert the initial state into an acceptable goal state. Unfortunately, not all games are so simple.

To begin with, there is the indeterminacy that arises in games with multiple players. Recall that the state in a game at each point in time can depend on the actions of other players, and keep in mind that no player knows those actions in advance. Of course, in some cases, it is possible for a player to find sequences of actions guaranteed to achieve a goal state no matter what actions are taken by the other players. However, such cases are quite rare. More often, it is necessary to create conditional plans in which a player's future actions are determined by its earlier actions and those of the other players. For such cases, more complex planning techniques are necessary.

Unfortunately, even this is not always sufficient. In some cases, there may be no guaranteed plan at all, not even a conditional plan. Tic-Tac-Toe is a game of this sort. Although it can be won, there is no guaranteed way to win in general. It is not really clear what to do in such situations. The key to winning is to move and hope that the moves of the other players put the game into a state from which a guaranteed win is possible. However, this strategy leaves open the question of which moves to make prior to arrival at such a state. One can fall back on probabilistic reasoning. However, this is not wholly satisfactory since there is no justifiable way of selecting a probability distribution for the actions of the other players. Another approach, of primary use in directly competitive games, is to make moves that create more search for the other players so that there is a chance that time limitations will cause those players to err.

Another complexity is the existence of resource bounds. In Tic-Tac-Toe, there are approximately 5000 distinct states. This is large but manageable. In Chess there are more than 10³⁰ states. A state space of this size, being finite, is fully searchable in principle but not in practice. Moreover, the time limit on moves in most games means that players must select actions without knowing for sure whether they are any good.

In such cases, the usual approach is to conduct partial search of some sort, examining the game tree to a certain depth, evaluating the possible outcomes at that point, and choosing actions accordingly. Of course, this approach relies on the availability of an evaluation function for non-terminal states that is roughly monotonic in the actual probability of achieving a goal. While, for specific games, such as chess, programmers are able to build in evaluation functions in advance, this is not possible for general game playing, since the structure of the game is not known in advance. Rather, the game player must analyze the game itself in order to find a useful evaluation function.

Another approach to dealing with size is abstraction. In some cases, it is possible to reformulate a state graph into a more abstract state graph with the property that any solution to the abstract problem has a solution when refined to the full state graph. In such cases, it may be possible to find a guaranteed solution or a good evaluation function for the full graph. Various researchers have proposed techniques along these lines, but more work is needed.

1.6 Discussion

While general game playing is a topic with inherent interest, work in this area has practical value as well. The underlying technology can be used in a variety of other application areas, such as business process management and computational law. In fact, many games used in competitions are drawn from such areas.

General Game Playing is a setting within which AI is the essential technology. It certainly concentrates attention on the notion of specification-based systems (declarative systems, self-aware systems, and, by extension, reconfigurable systems, self-organizing systems, and so forth). Building systems of this sort dates from the early years of AI.

It was in 1958 that John McCarthy invented the concept of the "advice taker". The idea was simple. He wanted a machine that he could program by description. He would describe the intended environment and the desired goal, and the machine would use that information in determining its behavior. There would be no programming in the traditional sense. McCarthy presented his concept in a paper that has become a classic in the field of AI.

The main advantage we expect the advice taker to have is that its behavior will be improvable merely by making statements to it, telling it about its environment and what is wanted from it. To make these statements will require little, if any, knowledge of the program or the previous knowledge of the advice taker.

An ambitious goal! But that was a time of high hopes and grand ambitions. The idea caught the imaginations of numerous subsequent researchers -- notably Bob Kowalski, the high priest of logic programming, and Ed Feigenbaum, the inventor of knowledge engineering. In a paper written in 1974, Feigenbaum gave his most forceful statement of McCarthy's ideal.

The potential use of computers by people to accomplish tasks can be "one-dimensionalized" into a spectrum representing the nature of the instruction that must be given the computer to do its job. Call it the what-to-how spectrum. At one extreme of the spectrum, the user supplies his intelligence to instruct the machine with precision exactly how to do his job step-by-step. ... At the other end of the spectrum is the user with his real problem. ... He aspires to communicate what he wants done ... without having to lay out in detail all necessary subgoals for adequate performance.

Some have argued that the way to achieve intelligent behavior is through specialization. That may work so long as the assumptions one makes in building such systems are true. For general intelligence, however, general intellectual capabilities are needed, and such systems shoud be capable of performing well in a wide variety of tasks. To paraphrase the words of Robert Heinlein.

A human being should be able to change a diaper, plan an invasion, butcher a hog, conn a ship, design a building, write a sonnet, balance accounts, build a wall, set a bone, comfort the dying, take orders, give orders, cooperate, act alone, solve equations, analyze a new problem, pitch manure, program a computer, cook a tasty meal, fight efficiently, die gallantly. Specialization is for insects.

It is our belief that general game playing offers an interesting application area within which general AI can be investigated.

Exercises

Exercise 1.1: Consider the following games. (Information about the games can be found on Wikipedia.)

Exercise 1.2: Connect to Gamemaster at http://gamemaster.stanford.edu using your favorite browser. Click the Games link and look at some of the games recorded there. Click the Standalone link for one of the games to play a match of that game. Repeat for a few other games. The point of the exercise is to become familiar with the Gamemaster system and get some experience learning and playing new games.